
The equivalent circuit of a solar cell
/wiki/File:Photovoltaic_cell.svg">
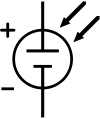
The schematic symbol of a solar cell
To understand the electronic behavior of a solar cell, it is useful to create a model which is electrically equivalent, and is based on discrete electrical components whose behavior is well known. An ideal solar cell may be modelled by a
current source in parallel with a diode; in practice no solar cell is ideal, so a shunt resistance and a series resistance component are added to the model. The resulting equivalent circuit of a solar cell is shown on the left. Also shown, on the right, is the schematic representation of a solar cell for use in circuit diagrams.
Characteristic equation
From the equivalent circuit it is evident that the current produced by the solar cell is equal to that produced by the current source, minus that which flows through the diode, minus that which flows through the shunt resistor:- I = IL − ID − ISH
- I = output current (amperes)
- IL = photogenerated current (amperes)
- ID = diode current (amperes)
- ISH = shunt current (amperes).
- Vj = V + IRS
- Vj = voltage across both diode and resistor RSH (volts)
- V = voltage across the output terminals (volts)
- I = output current (amperes)
- RS = series resistance (Ω).
- I0 = reverse saturation current (amperes)
- n = diode ideality factor (1 for an ideal diode)
- q = elementary charge
- k = Boltzmann's constant
- T = absolute temperature
- At 25°C,
 volts.
volts.
- RSH = shunt resistance (Ω).
In principle, given a particular operating voltage V the equation may be solved to determine the operating current I at that voltage. However, because the equation involves I on both sides in a transcendental function the equation has no general analytical solution. However, even without a solution it is physically instructive. Furthermore, it is easily solved using numerical methods. (A general analytical solution to the equation is possible using Lambert's W function, but since Lambert's W generally itself must be solved numerically this is a technicality.)
Since the parameters I0, n, RS, and RSH cannot be measured directly, the most common application of the characteristic equation is nonlinear regression to extract the values of these parameters on the basis of their combined effect on solar cell behavior.
Open-circuit voltage and short-circuit current
When the cell is operated at open circuit, I = 0 and the voltage across the output terminals is defined as the open-circuit voltage. Assuming the shunt resistance is high enough to neglect the final term of the characteristic equation, the open-circuit voltage VOC is:Effect of physical size
The values of I0, RS, and RSH are dependent upon the physical size of the solar cell. In comparing otherwise identical cells, a cell with twice the surface area of another will, in principle, have double the I0 because it has twice the junction area across which current can leak. It will also have half the RS and RSH because it has twice the cross-sectional area through which current can flow. For this reason, the characteristic equation is frequently written in terms of current density, or current produced per unit cell area:- J = current density (amperes/cm2)
- JL = photogenerated current density (amperes/cm2)
- J0 = reverse saturation current density (amperes/cm2)
- rS = specific series resistance (Ω-cm2)
- rSH = specific shunt resistance (Ω-cm2).
There are practical limitations of this formulation. For instance, certain parasitic effects grow in importance as cell sizes shrink and can affect the extracted parameter values. Recombination and contamination of the junction tend to be greatest at the perimeter of the cell, so very small cells may exhibit higher values of J0 or lower values of RSH than larger cells that are otherwise identical. In such cases, comparisons between cells must be made cautiously and with these effects in mind.
This approach should only be used for comparing solar cells with comparable layout. For instance, a comparison between primarily quadratical solar cells like typical crystalline silicon solar cells and narrow but long solar cells like typical thin film solar cells can lead to wrong assumptions caused by the different kinds of current paths and therefore the influence of for instance a distributed series resistance rS.
![I_{D} = I_{0} \left\{\exp\left[\frac{qV_{j}}{nkT}\right] - 1\right\}](http://upload.wikimedia.org/math/b/8/d/b8d0ebea3f33be0c023cf7b8a30cb717.png)
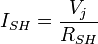
![I = I_{L} - I_{0} \left\{\exp\left[\frac{q(V + I R_{S})}{nkT}\right] - 1\right\} - \frac{V + I R_{S}}{R_{SH}}.](http://upload.wikimedia.org/math/4/7/d/47d17d3c2fe8840d0b3181860bd22f0a.png)


![J = J_{L} - J_{0} \left\{\exp\left[\frac{q(V + J r_{S})}{nkT}\right] - 1\right\} - \frac{V + J r_{S}}{r_{SH}}](http://upload.wikimedia.org/math/6/d/1/6d1690ed4b41c1e3d27569b0877a6b73.png)
I want say that this article is very nice and very informative article.I will make sure to be reading your blog more.
ReplyDeleteInstalling Solar Power
Solar Pool Heating
Solar Las Vegas
Solar Power Installation Companies
Please make sure that u don't copy out the content from wikipedia
ReplyDeleteThank you for sharing such an insightful article. People have questions regarding number of batteries for solar system if you have questions, please read this article to solve all your doubts.
ReplyDelete"Solar Panels Installation
ReplyDelete" Solar Panels Installer – Smart House Solar Company, Solar panel installation and Solar System companies in Australia.
solar resco model
ReplyDeleteThis comment has been removed by the author.
ReplyDeletesolar epc companies in india
ReplyDeletesolar panel manufacturing company in india
Thanks for this information; I hope it will use much reader who looking you regularly likes me…
ReplyDeleteRegards, How to know about active passive Components
If you are looking for Patch Cords, then we can confidently tell you that you are at the right place. UBIQCOM are the manufacturer and supplier of a wide range of Patch Cords product in multi-range. Contact us for one-stop solutions! Call +91 9910771797.
ReplyDeleteNice blog, it provides many informative and helpful articles. Thanks for sharing the information. Looking for more updates in future.
ReplyDeletesolar panel installers Ramsgate
Your posts always manage to brighten my day! I genuinely enjoy seeing them in my feed, If you are looking for reliable Solar Energy Company in Tamarac FL ? Right Plan Solar has got you covered! As your trusted solar brokers, we help you navigate through the options and choose the best solar financing plan tailored to your needs. Our expertise extends to solar installation service in Tamarac, FL, where our skilled professionals ensure a flawless installation process.
ReplyDeleteAn fxs voip gateway is a device that allows businesses to connect their analog phone lines to a VoIP network. FXO stands for Foreign Exchange Office, and it refers to the interface that receives dial tone,
ReplyDeleteThank you for sharing! Your article was a great read—I'm eagerly anticipating more content from you in the future.
ReplyDeletesolar panel installation company
Thanks for this information; I hope it will use much reader who looking you regularly likes me… Solar Pool Heating Perth
ReplyDeleteImmerse yourself in the vibrant world of Indian digital content with our exclusive YouTube subscriber purchase service. Grow your audience with a simple, economical transaction in rupees, facilitating the seamless addition of genuine subscribers to your channel. As your subscriber base blooms, so does the potential for your videos to go viral within the bustling Indian online community. Our service promises an increase in your channel's authority, inviting higher levels of interaction and engagement from your viewers. Enjoy the fruits of a flourishing YouTube channel without the worry of high expenses, as affordability meets effectiveness in our subscriber acquisition package. Enhance your digital presence, engage with an avid Indian audience, and watch your creativity take root across this lively content-sharing platform.
ReplyDeletehttps://www.buyyoutubesubscribers.in/
In the bustling metropolis of Mumbai, the Breast Specialist Lady Doctor stands as a pillar of strength and hope for those combating breast cancer. Her approach is holistic and patient-centric, focusing on both the physical and emotional aspects of care. With a profound understanding of the nuances of breast health, she utilizes the latest in medical advancements to tailor treatment options to each patient's unique situation. Her dedication extends beyond the clinical, offering support and advocating for her patients' overall well-being. Her practice is not just about treating the disease but empowering women through education and compassionate care. This specialist's commitment to excellence and empathy makes her an invaluable ally in the fight against breast cancer in Mumbai.
ReplyDeletehttps://drnitanair.com/
In the heart of Ahmedabad, a Colorectal Cancer Specialist is redefining patient care with unparalleled dedication and expertise. This specialist stands at the forefront of medical innovation, employing the latest advancements in treatment and diagnostic technologies. Their approach is deeply rooted in understanding the individual needs of each patient, crafting personalized care plans that address the physical, emotional, and psychological aspects of battling colorectal cancer. With a firm commitment to advancing research and incorporating holistic treatment methodologies, this professional goes beyond conventional care, striving to enhance the quality of life for those afflicted. The Colorectal Cancer Specialist in Ahmedabad embodies hope, offering not just treatments, but a chance for a renewed life beyond cancer.
ReplyDeletehttps://drvirajlavingia.com/
The Breast Specialist Doctor in Gurgaon emerges as a paramount figure in the fight against breast cancer, blending unparalleled medical expertise with heartfelt compassion. Anchored in the latest scientific research and technological advancements, this professional employs state-of-the-art diagnostic tools and treatment methods to ensure the most effective care for their patients. Their approach is deeply empathetic, recognizing the emotional turmoil breast cancer can evoke, and providing a supportive space where patients feel understood and valued. This specialist's dedication to personalized care ensures that each treatment plan is meticulously tailored to fit the individual’s unique condition and circumstances. Beyond the clinic walls, their commitment extends to raising awareness and educating the community on breast health, underscoring their role as not just a healthcare provider, but a beacon of hope and empowerment.
ReplyDeletehttps://www.breastoncosurgery.com/
In the dynamic landscape of Australian digital marketing, one SEO company rises above the rest with its innovative and result-driven strategies. This firm combines the power of advanced analytics, comprehensive keyword research, and creative content solutions to propel businesses to the forefront of online searches. Their tailored approach ensures that each client's unique needs and goals are met with precision and excellence. By focusing on sustainable growth and maximum online visibility, they help Australian businesses not only achieve but sustain top rankings in search engine results. Their commitment to transparency and client education demystifies the complexities of SEO, making them a trusted partner in the competitive digital arena.
ReplyDeletehttps://digiquakesolutions.com/
Best Solar Panels in Sydney, Australia
ReplyDeleteThis article provides a thorough explanation of the equivalent circuit model for solar cells, breaking down the key components such as the current source, diode, series resistance, and shunt resistance. It offers a clear understanding of how these elements interact to determine the solar cell’s performance. The characteristic equation and its practical implications, including the impact of cell size, are well-explained. Overall, this piece serves as a valuable resource for anyone seeking to understand the fundamental electrical behavior of solar cells and the factors influencing their efficiency.
ReplyDeleteEnphase Micro Inverter
Ak hľadáte miesta, kde môžete pridať komentár s odkazom na vašu stránku https://www.slovaksolar.com/ pre kľúčové slovo Fotovoltaika, odporúčam zvážiť nasledujúce kroky:
ReplyDelete